It's commonly known that reliability analysis is based on evaluating previous failures of a system to calculate statistical patterns that help predict the future behavior of equivalent systems. However, it's not only failures we are interested in when characterizing our system, as it's just as useful to know when a sample fails as it is to know when it doesn't. That is not to say that analyses made with only failures as their input data are wrong — nothing further from the truth. In fact, these tend to be the most common. However, non-failed samples are very helpful sometimes, as we are about to see.

What is a suspension

Imagine you set up a lab test with 30 samples of a system that have been cycling over and over for a couple of months, out of which 25 have failed, and 5 still remain functional. According to your schedule, you need to finish the test already and calculate its results, or you'll be running late for the next phase of your project. So, you decide to stop it. You've probably guessed it by now: those five functional samples are suspensions.

Some people may think, "Well, if those samples haven't failed, how can they be of use in calculating the probability of failure of the system?". The answer is easy: if one simply ignored the suspensions, they would be misrepresenting the test's behavior, as it would seem like only 25 samples were tested, and all of them had failed within the given time.

How are suspensions treated in the calculations

Without the need for entering into too much detail, the difference between failures and suspensions when it comes to how they are used to perform the distribution calculations is as follows:

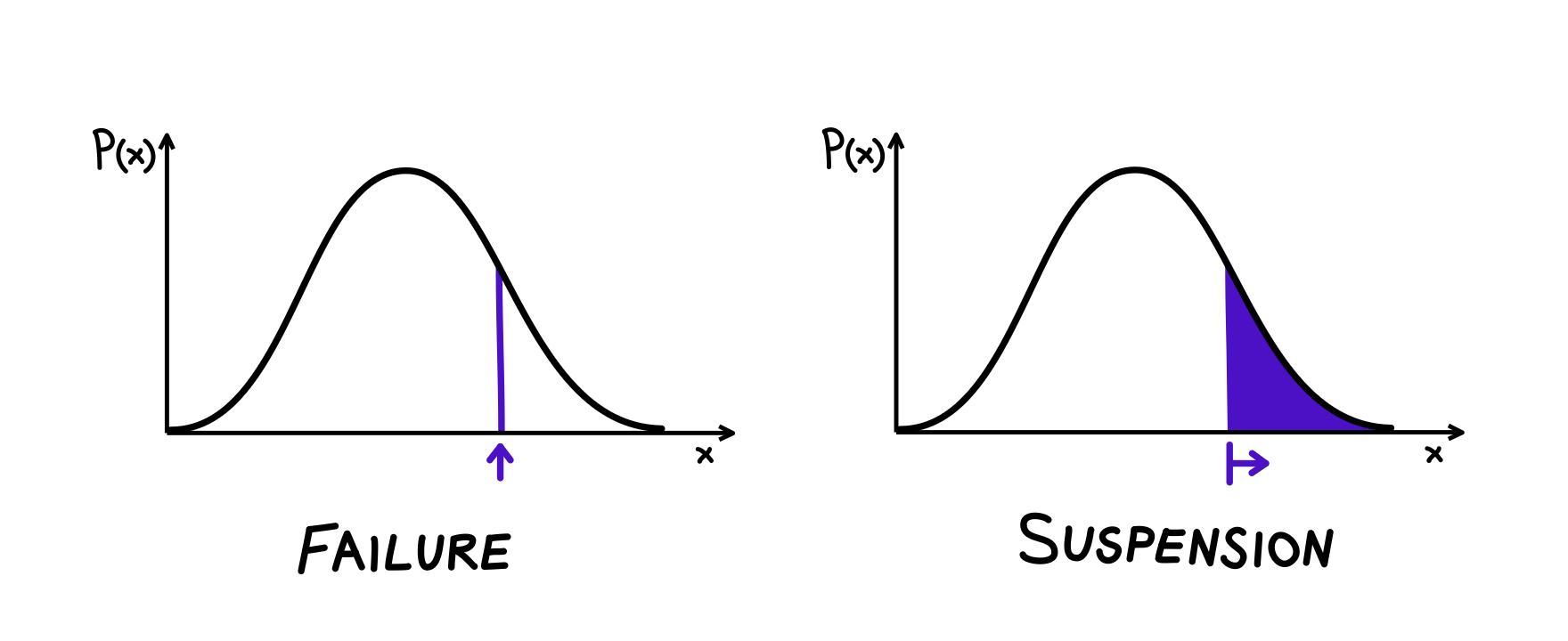
• Failures: for a given distribution, what is the likelihood of experiencing a failure at this exact time?
• Suspensions: for a given distribution, what is the likelihood of experiencing a failure after this exact time?

Suspensions shouldn't be abused

It is great that suspensions can be included in the calculations instead of ignoring their impact on the results or having to wait for those samples to fail to complete the test. Furthermore, adding them to our calculations not only benefits the representativity of the system's behavior but also tends to narrow the width of the confidence bounds, even when they are not failures. However, the use of too many suspensions, and more specifically, their proportion to the number of failures, could taint the results, as the information they add to the calculations is more vague than that of a specific moment of failure.

The trap of early suspensions

In the example above, the suspensions resulted from finishing a test before all the samples had failed, and thus, all the suspension values were equal to or greater than the largest of the failure times. However, other scenarios may lead to obtaining suspended samples, such as the need to use one of the tested samples for other purposes, thereby removing it from the experiment. This situation would produce a sample that lasted a certain number of test cycles without failing, and should rightfully be treated as a suspension.

Nevertheless, as we saw in the image above, if the suspension is initiated very early in time, the information it contributes to the calculations is limited, as it's not uncommon for a sample removed early in the test to have survived it. Another way of encountering early suspensions is when dealing with on-the-field systems. Unlike a lab test that typically starts testing all the samples at once, on-the-field systems tend to begin their use period at different times. Consequently, some samples may have been lightly used at the time of performing the analysis.

When to use suspensions

As a rule of thumb, the more failures, the better, as failures contribute precise data to the calculations. However, it's rare to find ourselves in a situation where we have all the data we need in the ideal format—considering budgets, schedules, and other constraints. In reality, we often have to work with the resources available to us.

Suspensions should be regarded as valuable pieces of information for our study and can significantly improve the accuracy of our results, especially when they occur late in the test.